A few years back, I stumbled upon a paper by Prof. Katepalli R. Sreenivasan, "Chandrasekhar's Fluid Dynamics" [1], where I first read about Quantum fluids. As someone deeply passionate about turbulence and spending quite some time understanding the Quantum mechanics phenomenon at BQP, I thought to jot down some fundamentals of this area. The article aims to get the readers interested in the area of Quantum fluids/turbulence and how it relates to classical fluid mechanics. I will conclude this with a thought of whether Quantum fluid behavior can help us solve the last unsolved problem of classical physics - turbulence in viscous fluids.
What are Quantum Fluids?
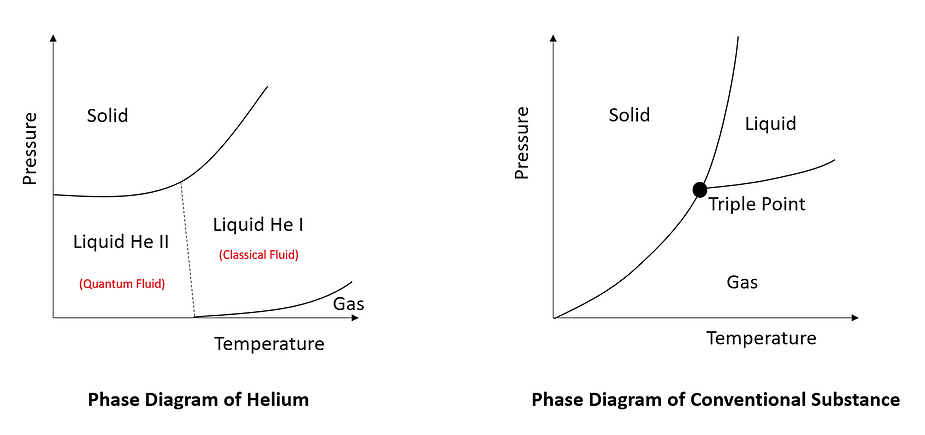
Quantum fluids are liquids that exhibit quantum properties at sufficiently low temperatures. One such fluid is the liquid Helium (He I). Usually, a phase change diagram of a conventional substance displays a triple point (TP) - where solid, liquid, and gas coexist. If you look at the phase diagram of liquid Helium (shown below), it is significantly different from that of a conventional liquid. In the phase diagram of liquid Helium, the curve undergoes a discontinuity (due to the change in the shape of the curve). This behavior is called a lambda transition which is characteristic of a phase change. Hence, we should expect two phases, Helium I (He I) and Helium II (He II). It was experimentally noted that Helium II is a liquid even at absolute zero (at atmospheric pressure). Hence, Helium II was coined "superfluid." The most important property of this fluid is its ability to flow without viscosity.
Relation between Quantum Fluids and Classical Fluids
The behavior of Quantum fluids can be described by a particular type of nonlinear Schrodinger equation called Gross-Pitaevskii Equation (GPE). For a condensate in a homogenous system, it can be written as follows:

By using Madelung transformation,

and defining fluid velocity field as follows:

Putting this into GPE and after certain mathematical manipulations, this becomes as follows:

Equation 4 is precisely the classical continuity equation. Equation 5 is similar to the classical Euler equation for inviscid fluid except for the last term on the right-hand side. The last term comes from quantum pressure, which makes this equation different from the classical momentum equation. It is essential to realize that even though viscosity in quantum fluids is zero, this quantum pressure term (similar to the viscous term in the classical momentum equation) leads to the phenomenon of turbulence in quantum fluids.
Concluding Remarks
Let's understand the vortex behaviors in the two fluids. In classical fluids, a vortex is marked by a region where fluid revolves around an axis line (given by curl of local velocity). Vortices are generated due to the system's inherent instability and are unstable, i.e., their structures can change over time, and the value of the vorticity can be arbitrary. Compared to that, quantum fluids exhibit different behavior. Taking the expression from Equation 3, it can be seen that the curl of this velocity field will become zero. This means that circulation around a path surrounding a topological defect (the discrete points in space where ψ vanishes) is either zero or a multiple of the quantum of circulation. Hence, a vortex in Quantum fluids is a line-like object in 3D, with its structures and vorticities being definite. Hence, the structure of the quantum vortex is much simpler than its classical counterpart.
A last interesting aspect of Quantum turbulence that I wanted to touch upon is its two energy spectrums of turbulence. In the first regime (quasi-classical turbulence), the energy spectrum obeys the same Kolmogorov scaling as shown by classical fluids. In the second regime (ultra-quantum turbulence), the energy spectrum follows the Kelvin waves cascade.
It is clear that Quantum fluid creates turbulence because of quantized vortices due to mutual friction by excitation. This leads to an effective kinematic viscosity that has the same units and scale as that of viscosity in classical fluids. But this is purely a numerical coincidence! Nonetheless, an important area to investigate.
Thank you for reading! Please share your thoughts in the comments.
Note: All images and equations have been self-produced. The references of these images, equations, and texts are picked up from the following resources:
[1] Sreenivasan, Katepalli R. "Chandrasekhar's Fluid Dynamics." Annual Review of Fluid Mechanics 51 (2019): 1-24.
[2] Barenghi, Carlo F., and Nick G. Parker. A primer on quantum fluids. Berlin: Springer, 2016.
[3] La Mantia, M., and L. Skrbek. "Quantum, or classical turbulence?." EPL (Europhysics Letters) 105.4 (2014): 46002.
[4] Skrbek, Ladislav, and Katepalli R. Sreenivasan. "How similar is quantum turbulence to classical turbulence?." Ten Chapters in Turbulence. Cambridge University Press, 2010. 405-4
[5] Wang, Xueying. "Quantum Turbulence, and How it is Related to Classical Turbulence." (2018).




.png)
.png)


%201.svg)
.svg)
.svg)
.svg)
.svg)
.svg)




