The Limitations of Classical Optimization

In aerospace and automotive engineering, designing high-performance airfoils demands balancing weight reduction, structural integrity, and aerodynamic efficiency. Traditional topology optimization methods, reliant on finite element (FE) analysis, often struggle with computational complexity, slow convergence, and vague design boundaries. Enter BQPhy—BQP's cutting-edge Quantum-Inspired Solver powered by Quantum-Inspired Evolutionary Optimization (QIEO) Algorithms—to redefine efficiency in engineering.

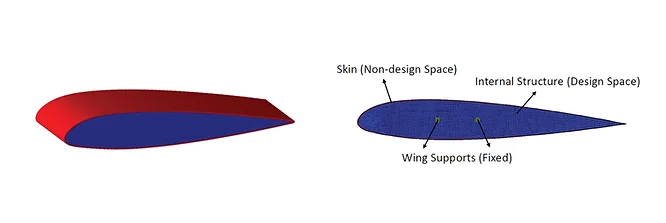
Figure 1: Schematic Airfoil section internal domain as design space, the outer skin as non-design space, and the wing supports are fixed.

What is BQPhy’s QIEO Algorithm?

‍
BQPhy’s optimization engine leverages quantum inspired algorithms —to transform computational problem-solving. Unlike classical methods, which evaluate solutions sequentially, QIEO Algorithms explore vast solution spaces simultaneously. This enables:

• Faster convergence to optimal designs.
• Global optima identification, avoiding local minima traps.
• Reduced computational resource usage, cutting costs and time.

BQP’s BQPhy Solver integrates QIEO Algorithms to tackle complex challenges like airfoil volume minimization. By emulating quantum parallelism, QIEO delivers precision unattainable with classical techniques.

‍

Figure 2: The figure illustrates how, in the real world, the origin of aerodynamic forces on an airfoil section arises from the combined effects of pressure distributions and shear stress on the boundary layer.

Why QIEO Outperforms Classical Topology Optimization
‍

Traditional methods rely on FE analysis, treating each element as a continuous variable (0–1). This creates ambiguous boundaries and “fictitious” material zones, complicating fabrication. BQPhy’s QIEO Algorithms address these flaws by:

1. Handling 70,000–100,000 variables efficiently, typical in wing-structure optimization.
2. Producing clear, manufacturable designs with defined material distributions.
3. Slashing simulation time via fewer iterations.

Traditional topology optimization problems are typically solved using finite element (FE) analysis, treating each element's presence as a design variable and aiming to find the optimal distribution of elements in the design domain [4]. This approach formulates the problem with continuous design variables, where design variables take values from 0 to 1. They produce optimal designs with fictitious elements and no clear boundary for fabricating them [4, 5].  

Previous research has demonstrated that efficient topology optimization techniques can significantly enhance aircraft performance and safety. For example, Airbus's method successfully reduced the weight of A380 components such as wingbox ribs by 10%, leading to increased stability, safety, and a 42% reduction in drag. These advancements in topology optimization have also led to cost reductions for aircraft manufacturing companies. However, for a middle-sized topology optimization problem on flexible wing structures, the number of design variables can reach up to approximately 70,000 to 100,000, making these problems incredibly complex for traditional optimization methods [2, 6].  

With the QIEO (Quantum-Inspired Evolutionary Optimization) Algorithms , topology optimization achieves highly optimized results for internal aircraft wing structures, improving efficiency and reducing manufacturing costs. The solver can handle complex design problems, such as minimization of the total weight of the structure, and finds global minima for obtaining optimal airfoil designs.  

BQPhy’s topology optimization results for airfoil wings using QIEO have demonstrated remarkable outcomes. By considering the outer skin as a non-design domain, the weight of the airfoil structure can be reduced to 60% [refer to Figure 3] of its initial solid volume while maintaining its structural integrity.  

Key Benefits of BQPhy in Airfoil Design

1. Weight Minimization: Achieve ultra-light structures without compromising strength.
2. Cost-Effectiveness: Lower compute resource needs translate to budget-friendly R&D.
3. Performance Enhancement: Optimized aerodynamics for fuel efficiency and speed.
4. Fabrication-Ready Results: Binary material distribution eliminates guesswork.

The Future of Engineering with BQPhy
‍

‍BQPhy’s QIEO Algorithms emerge as the definitive solution.  

Ready to revolutionize your design process? Discover how  QIEO Algorithms can elevate your next project.

‍

‍List of references:  

1. Zhu, Ji-Hong, Wei-Hong Zhang, and Liang Xia. "Topology optimization in aircraft and aerospace structures design." Archives of computational methods in engineering 23 (2016): 595-622.  

2. Luis Félix, Alexandra A. Gomes2, and Afzal Suleman. “Wing Topology Optimization with Self-Weight Loading” iWorld Congress on Structural and Multidisciplinary Optimization May19, -24, 2013, Orlando,Florida, USA.  

3. Stanford, Bret, and Peter Ifju. "Multi-objective topology optimization of wing skeletons for aeroelastic membrane structures." International Journal of Micro Air Vehicles 1.1 (2009): 51-69.  

4. Høghøj, Lukas C., et al. "Simultaneous shape and topology optimization of wings." Structural and Multidisciplinary Optimization 66.5 (2023): 116.  

5. Gomes, Pedro, and Rafael Palacios. "Aerodynamic-driven topology optimization of compliant airfoils." Structural and Multidisciplinary Optimization 62 (2020): 2117-2130.  

6. James, Kai. Aerostructural shape and topology optimization of aircraft wings. University of Toronto (Canada), 2012.